Grover's quantum algorithm

Quantum quadratic speedup for unstructured search.

Grover's algorithm, also known as the quantum search algorithm, solves the unstructured search problem while also providing quadratic speedup.

The problem statement is as follows: given $LaTeX figure$ , $LaTeX figure$ and a function $LaTeX figure$ which outputs 0 for all but one input value, find the value $LaTeX figure$ for which $LaTeX figure$ . A classical computer could solve this problem with a time complexity of $LaTeX figure$ , as it needs to evaluate the function $LaTeX figure$ times on average. However, as we will see in the following paragraphs, Grover's algorithm provides quadratic speedup, effectively succeeding in finding $LaTeX figure$ with a time complexity of $LaTeX figure$ .

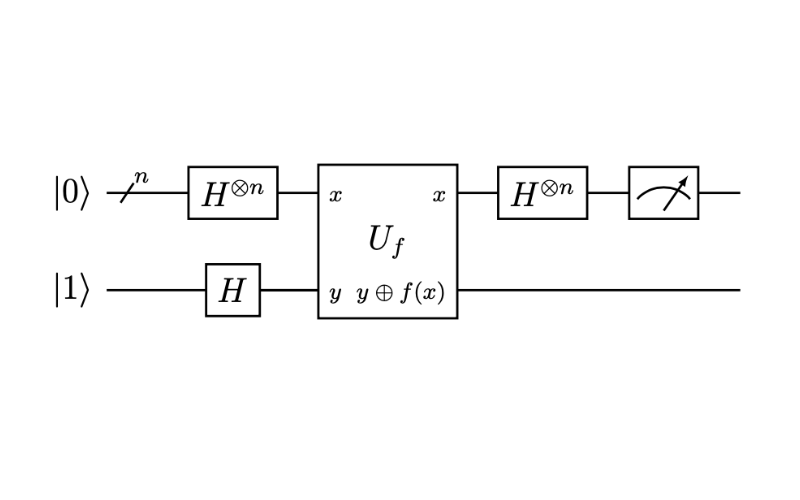
The quantum circuit that implements Grover's algorithm is shown below.

The quantum circuit is made up of $LaTeX figure$ qubits which initially are all in state $LaTeX figure$ . Let us define $LaTeX figure$ as the state of the quantum system after we apply the $LaTeX figure$ gate on each qubit.

$LaTeX figure$

We will hereafter denote by $LaTeX figure$ the superposition of all $LaTeX figure$ bitstrings $LaTeX figure$ of length $LaTeX figure$ . Let us not introduce $LaTeX figure$ . We can rewrite $LaTeX figure$ as

$LaTeX figure$

where $LaTeX figure$ [1].

Next, we apply the $LaTeX figure$ oracle. This oracle, also called a subrouting, is defined as $LaTeX figure$ . Hence, we obtain

$LaTeX figure$

The next step of the algorithm is the application of a diffuser $LaTeX figure$ . Using trigonometric identities, we obtain

$LaTeX figure$

After applying the successive $LaTeX figure$ and $LaTeX figure$ instructions, we reach

$LaTeX figure$

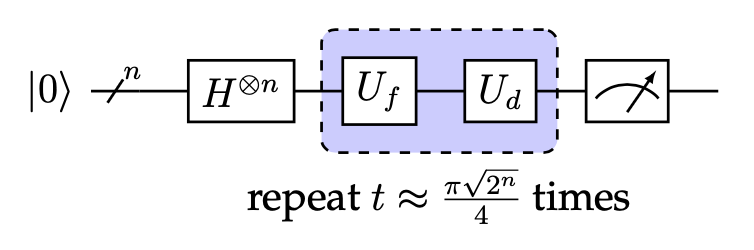
Let us apply these two gates $LaTeX figure$ times. After $LaTeX figure$ iterations, we obtain

$LaTeX figure$

After $LaTeX figure$ iterations, the probability to measure $LaTeX figure$ is

$LaTeX figure$

Supposing that $LaTeX figure$ is considerably larger than 1, the probability $LaTeX figure$ can be approximated as $LaTeX figure$ . When $LaTeX figure$ (i.e., $LaTeX figure$ ), the probability $LaTeX figure$ approaches 1. Hence, in order to obtain an answer with a high confidence, we must iterate over the $LaTeX figure$ and $LaTeX figure$ instructions $LaTeX figure$ times. This is what actually makes Grover's algorithm have a time complexity of $LaTeX figure$ : we evaluate the function $LaTeX figure$ approximately $LaTeX figure$ times using the $LaTeX figure$ oracle.

It has already been proven that Grover's algorithm's quadratic speedup is optimal for the unstructured search problem. This means that we cannot solve the problem in polynomial time or faster, even on a quantum computer. However, the time complexity of Grover's algorithm, which is $LaTeX figure$ , is still much better than the exponential time complexity of $LaTeX figure$ for a considerably large value of $LaTeX figure$ .

The SAT (i.e., boolean satisfiability) problem can be solved using this algorithm. Let us consider the following SAT instance [2], and implement it in KetBy.

$LaTeX figure$ open

By employing ancilla qubits, we can implement Grover's algorithm for $LaTeX figure$ as shown in the figure below.

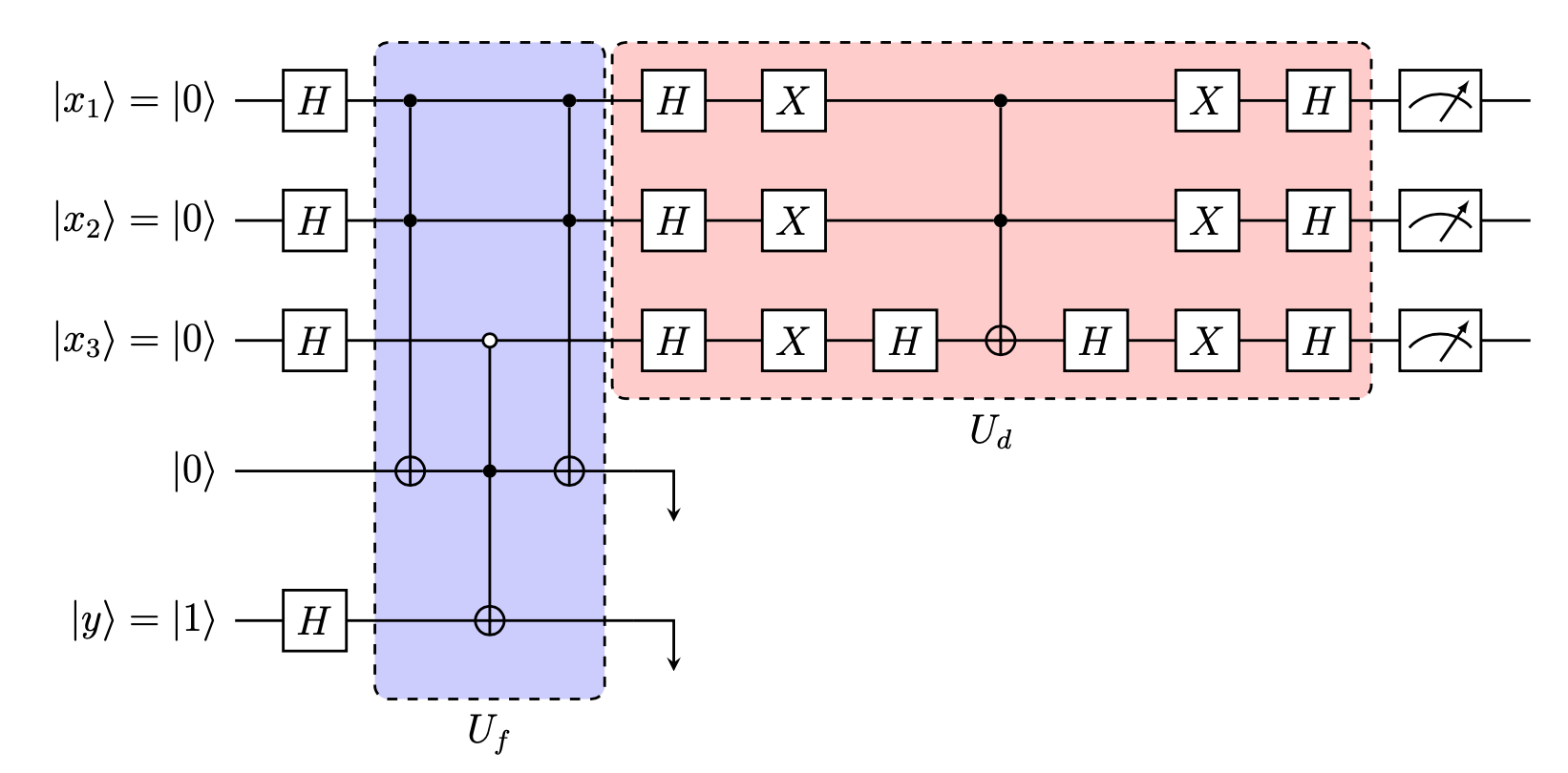
As we can see, we use two ancilla qubits to implement the oracle $LaTeX figure$ . The second ancilla qubit is initially in state $LaTeX figure$ and we apply a $LaTeX figure$ gate on it. We use $LaTeX figure$ gates to compute the conjunctions between the literals, effectively mapping $LaTeX figure$ to $LaTeX figure$ . We also undo the first $LaTeX figure$ gate (i.e., uncompute the first ancilla qubit). Finally, we apply the diffuser $LaTeX figure$ .

You can find a implementation of this circuit with $LaTeX figure$ and $LaTeX figure$ iterations here.

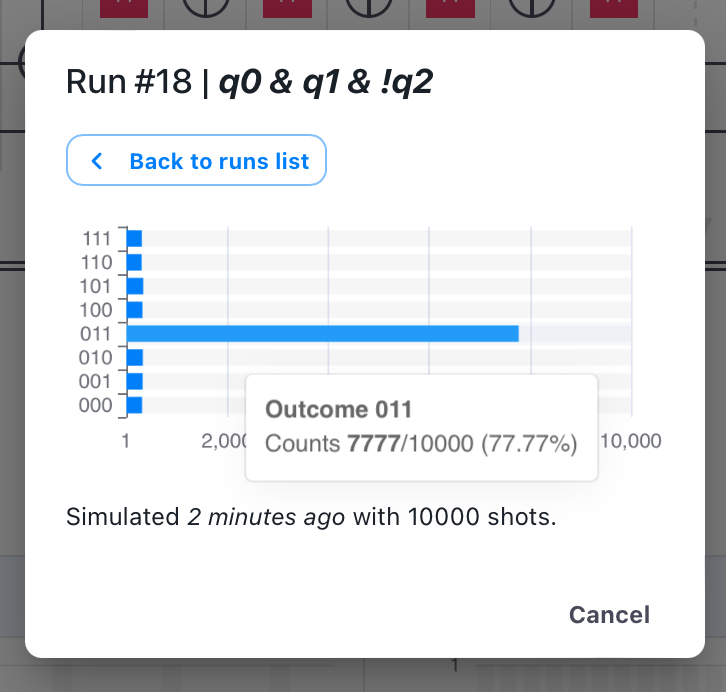
According to the previous introduction, $LaTeX figure$ is defined as $LaTeX figure$ . In our case, $LaTeX figure$ , hence $LaTeX figure$ . After $LaTeX figure$ iterations over the $LaTeX figure$ oracle and the $LaTeX figure$ diffuser, the probability to measure $LaTeX figure$ , where $LaTeX figure$ is the bitstring that encodes the solution to the SAT problem, is $LaTeX figure$ . When running a simulation of the circuit with $LaTeX figure$ iterations of $LaTeX figure$ and $LaTeX figure$ , we measure $LaTeX figure$ (where $LaTeX figure$ is the solution to the problem) in $LaTeX figure$ of the cases, as shown below.

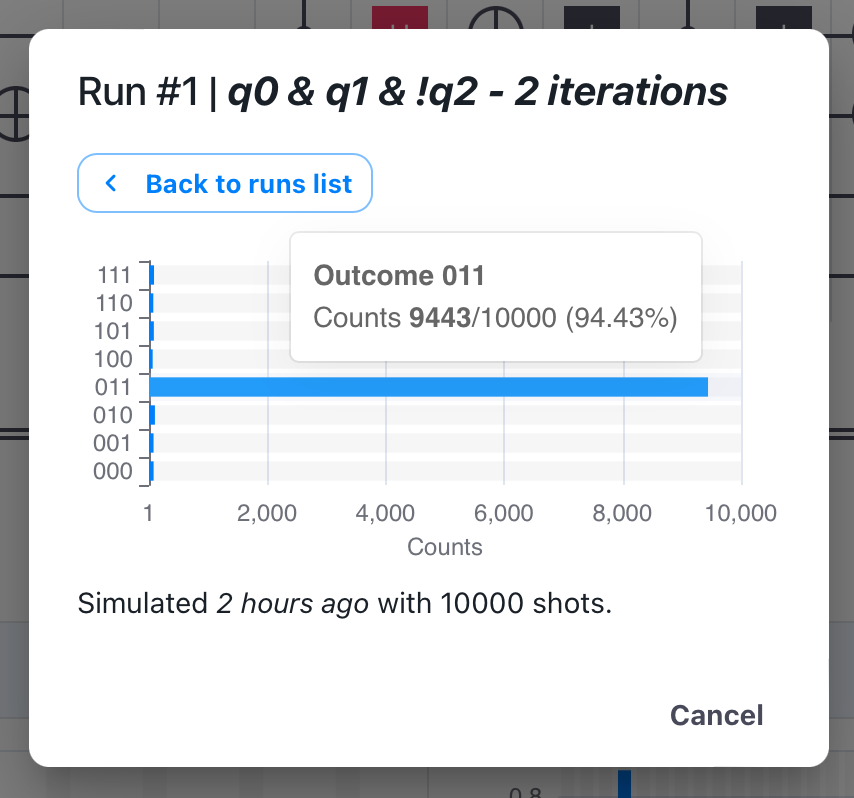
Let us now perform two iterations over $LaTeX figure$ and $LaTeX figure$ . In this case, the probability of success is $LaTeX figure$ . Again, the results of the simulation correlate with the mathematically expected results, as we measure the state $LaTeX figure$ in $LaTeX figure$ of the cases.

Grover circuit example with 2 iterations

References

[1] B. Vermersch, Lecture notes on "Quantum algorithms", Université Grenoble Alpes 2023, URL: https://bvermersch.github.io

[2] B. Siegelwax, Grover's Algorithm, an Intuitive Look, Quantum Zeitgeist 2021, URL: https://quantumzeitgeist.com/grovers-algorithm-an-intuitive-look/

Grover's quantum algorithm

Quantum quadratic speedup for unstructured search.

Related articles - see all