The Deutsch-Jozsa quantum algorithm

From exponential to constant time complexity using quantum speedup.

The Deutsch-Jozsa quantum algorithm solves a very specific problem which, although has little to no practical use, was among the first to show the speedup of quantum computing over classical computing.

The problem statement is as follows: given a boolean function $LaTeX figure$ , we must find out whether it is constant (i.e., $LaTeX figure$ ) or balanced (i.e., $LaTeX figure$ produces 1 on exactly half of the inputs $LaTeX figure$ ). We are promised it is either one or the other.

A classical computer would need $LaTeX figure$ evaluations of $LaTeX figure$ to yield a deterministic answer in the worst case. However, as we will see, the Deutsch-Jozsa quantum algorithm can yield the same answer with just one evaluation of $LaTeX figure$ .

The quantum circuit on which this algorithm runs requires $LaTeX figure$ qubits. The key of this algorithm is to find a way to implement $LaTeX figure$ as a quantum oracle $LaTeX figure$ that maps a state $LaTeX figure$ to $LaTeX figure$ , where $LaTeX figure$ denotes the bitwise exclusive-or (XOR) operator (alternatively, addition modulo 2).

A typical circuit implementing the Deutsch-Jozsa algorithm is shown below.

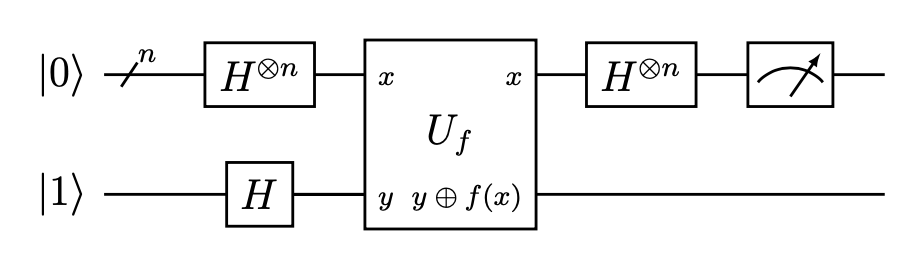
The quantum circuit has the initial state $LaTeX figure$ . Let us apply an $LaTeX figure$ gate on each of the $LaTeX figure$ qubits. This leads us to

$LaTeX figure$

In the equality above, the sum runs over all bitstrings of length $LaTeX figure$ . We then apply the quantum oracle $LaTeX figure$ to the circuit, which maps the state $LaTeX figure$ to $LaTeX figure$ . We obtain

$LaTeX figure$

which tells us that the first $LaTeX figure$ qubits are still is the same state as in the case of $LaTeX figure$ , but the qubit on position $LaTeX figure$ now successfully encodes $LaTeX figure$ .

We notice how, if $LaTeX figure$ , the state of the last qubit is $LaTeX figure$ . Similarly, if $LaTeX figure$ , the state of the last qubit is $LaTeX figure$ . For this reason, we can rewrite $LaTeX figure$ as

$LaTeX figure$

We may now ignore the last qubit and only focus on the first $LaTeX figure$ qubits. We are left with the following state:

$LaTeX figure$

Next, we apply the $LaTeX figure$ gate on the first $LaTeX figure$ qubits again. We obtain

$LaTeX figure$

In the expression above, $LaTeX figure$ is the sum of the bitwise product. Again, the sums in the expression of $LaTeX figure$ run over all bitstrings of length $LaTeX figure$ .

The last step of the algorithm involves measuring the first $LaTeX figure$ qubits. Given the state of $LaTeX figure$ , the probability of measuring $LaTeX figure$ is

$LaTeX figure$

We notice how, if $LaTeX figure$ (i.e., $LaTeX figure$ is constant), $LaTeX figure$ will evaluate to

$LaTeX figure$

In other words, if $LaTeX figure$ is constant, the probability to measure $LaTeX figure$ is 1. Similarly, if $LaTeX figure$ is balanced, then $LaTeX figure$ evaluates to 0, as any value of $LaTeX figure$ inside the sum will be canceled out by a value of $LaTeX figure$ . Therefore, if $LaTeX figure$ is balanced, any state other than $LaTeX figure$ will be measured.

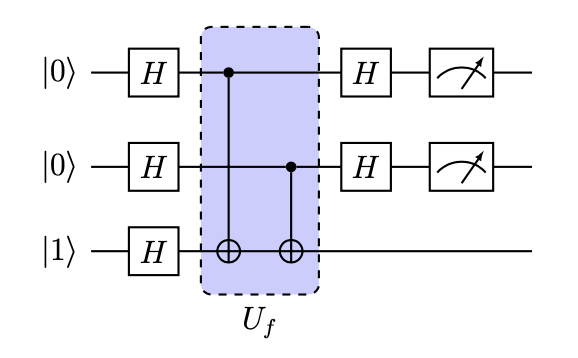
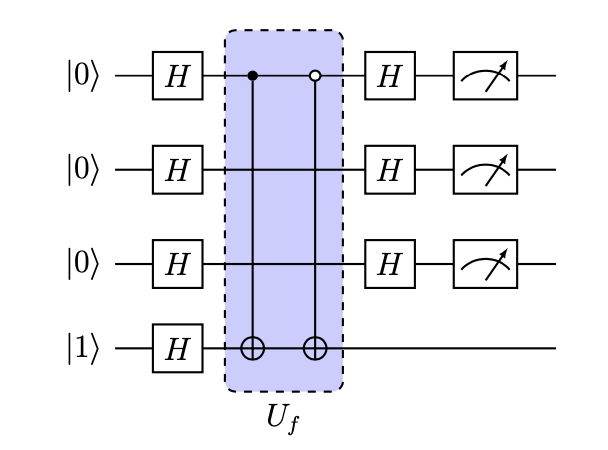
Check out the following examples implemented in KetBy.

$LaTeX figure$ open

$LaTeX figure$ is balanced

$LaTeX figure$ open

$LaTeX figure$ is constant

The Deutsch-Jozsa quantum algorithm

From exponential to constant time complexity using quantum speedup.

Related articles - see all